과학/창업

양자컴퓨터 알짜배기

큐비트와 양자 게이트 연산

전 단계 강의에서 비트, 전자 구름바퀴, Octet Rule, 반도체와 트랜지스터로 이진법 숫자 0과 1이 만들어지는 과정을 살펴 봤습니다. 0과 1을 사용하여 컴퓨터 언어 기계어를 만들지요.

컴퓨터는 단지 기계어 명령만 알아 먹습니다. 이런 컴퓨터를 고전컴퓨터라고 부릅니다.

이제 양자컴퓨터에서 이진법 0과 1을 어떻게 연산해 내는지를 살펴봅니다.

우선 양자의 상태를 먼저 개념 지어야 합니다.

개념을 짓는다는 것은 양자는 우리 눈으로 확인을 할 수가 없고, 단지 그 결과를 측정하여 확률적으로 인식을 해야 하기 때문입니다. 이 점이 아주 이해하기 힘든 대목입니다.

고전컴퓨터의 비트 0과 비트 1은 전기 스위치 트랜지스터(Transistor, TR)를 통하여 인식이 됩니다. 즉 TR On=Bit 1입니다. TR Off=Bit 0입니다. TR On은 불이 들어오고, TR Off는 불이 들어오지 않는 것을 눈으로 바로 볼 수 있습니다.

양자컴퓨터는 이런 방식으로 확인을 해 볼 수가 없습니다. 양자연산을 하여 측정을 하면 양자 상태가 붕괴되어, 0이나 1의 결과를 확인할 수가 없기 때문입니다.

다만 그 확률로만 인식을 해야 합니다. 확률이 나오니 통계학의 용어라 어렵게 여겨지지만 여기서는 쉽게 설명합니다.

지금부터 큐비트와 양자 게이트(Q Gate)가 양자 중첩, 양자 얽힘, 양자 연산하는 상태와 그 결과를 확률로 측정하는 과정을 설명합니다.

이 내용이 양자컴퓨터의 핵심 원리입니다. 양자컴퓨터의 알짜배기를 다루는 것입니다.

1. 큐비트의 양자 중첩 나타내기

큐비트는 디렉 표기법을 사용하여 | 0 > 과 | 1 > 로 표기하고, 각각 Ket 0 과 Ket 1 로 읽습니다. 그냥 둘 다 사용하면 됩니다.

양자 연산에서는 양자 상태(State)라는 개념을 먼저 이해해야 합니다. 양자는 파동이자 입자 입니다. 파동은 움직이는 상태이고, 입자는 움직이다가 어느 모습(입자)으로 정지해 위치를 가지는 상태 입니다. 그 움직임을 파동(Wave)이라고 하고, 정지한 위치를 위상(Phase)이라고 합니다.

그런데 눈으로 보이지는 않지만, 천재 과학자들이 실험으로 증명을 해보니 양자(Quantum)가 이런 상태라는 것입니다. 우리는 어떤 대상을 인식할 때 개념(Concept)으로 이해를 합니다. 그런 연유로 양자컴퓨터 설명에는 양자의 상태와 그 개념을 두루 사용합니다.

양자는 그 입자 상태와 파동 상태를 동시에 측정해 볼 수가 없습니다. 따라서 입자상태를 측정해 보면 파동상태를 알 수가 없고, 파동상태를 측정해 보면 입자상태를 알 수가 없습니다.

이런 어려운 원리를 불확정성 원리 이라고 합니다.

양자역학에는 유독 원리(Principle)가 많습니다. 너무 그 단어의 개념에 집착할 필요는 없고, 그런 것도 있구나 하고 넘어가도 양자컴퓨터 이해에는 지장이 없습니다.

양자는 중첩의 성질을 가집니다. 그 성질을 확인하기 위해서는, 선형대수학을 사용하여 증명해 냄으로써 인식을 합니다.

선행대수학에서는 행렬(Matrix)을 사용하여 큐비트를 나타냅니다. 큐비트 0은 행렬 (1 0)으로 표시합니다. 큐비트 1은 (0 1)로 나타냅니다. 이런 표기를 행행렬(가로 표기)이라고 합니다. 열행렬(세로 표기)을 더 많이 사용하는데, 스마트폰에서는 열행렬 세로 표기가 잘 안되기 때문에 여기서는 행행렬만 설명합니다.

열행렬은 행형렬로 나란히 표기하기도 합니다. 2행렬은 2X2 행렬로 표기하고, Tow by Tow Matrix라고 읽습니다. 열행렬의 앞 세로 숫자를 먼저, 다음에 뒤 세로 숫자 순으로 표기합니다. Ket 0(10)과 Ket 1(01) 2X2 세로 행렬은, 가로로 풀어서 (10 01) 처럼 표기합니다. 이런 행렬 표기법으로 큐비트는 선형대수학에서 행렬을 사용하여 나타냅니다.

행렬은 괄호를 사용합니다. 행렬이 두 행 두 열 이상이면 대괄호를 사용하고, 단일 행렬은 소괄호를 사용합니다.
큐비트 0=(1 0) 이고, 큐비트 1=(0 1) 입니다. (1X1) 행렬이라고 합니다. 양자 게이트는 (2X2), (3X3) 행렬도 사용합니다.

(2X2), (3X3)의 열행렬은 (앞 세로행렬X뒤 세로행렬) 형식으로 나타내야 하기 때문에’ 不肖 스마트폰 모니터로는 표기할 수가 없습니다. 이런 양자상태를 각각 선행대수 행렬곱으로 계산을 하기 때문에 그 개념만 이해하고 넘어 갑니다.

큐비트 중첩은 큐비트 0과 큐비트 1이 중첩되어 하나인 것처럼 작용하는 상태를 말합니다. 이를 선행대수 함수로 나타냅니다.

Ket Psi(희랍어 프사이)=[A (Ket 0)+ B(Ket 1])/루트 2, A 2승 + B/ 2승=1

Ket Psi는 큐비트 0과 동 1의 중첩을 나타내는 선형대수 함수명이고, A와 B는 그 상태 계수로서 각각의 확률을 나타냅니다. A와 B의 제곱합이 1이 된다는 것은 확률이 1이 된다는 것으로서, 큐비트 0과 큐비트 1이 동시에 있는 상태입니다.

동시에 있다는 것은 큐비트 0과 큐비트 1이 50%:50%으로 겹쳐 있다는 것 입이다. 이 50%가 큐비트가 존재하는 확률로서, 양자 큐비트의 존재 확률은 언제나 그 합이 1입니다. A=70%, B=30%인 경우도 나옵니다.

이해가 갑니까? 이해 안 가는 것이 정상입니다. 이해는 안 가지만 사실입니다.

이런 어려운 함수로 무엇을 하나요? 바로 다음 단계 양자 연산과 측정을 위한 사전 포석입니다.

2. 큐비트의 양자연산

큐비트의 양자연산은 양자 게이트에서 작동됩니다. 큐비트를 양자 게이트와 연결(입력)하여 양자 연산을 합니다. 그러려면 큐비트 HW와 양자 게이트 HW를 만들어야 합니다. 우선 양자 게이트를 먼저 설명합니다.

2-1. 양자 게이트 만들기
양자 게이트의 종류로는 큐비트 1개를 연결하는 단일 양자 게이트, 두 개를 연결하는 2 양자 게이트, 3 개를 연결하는 3 양자 게이트가 주를 이룹니다.

단일 양자 게이트는 파울리(Pauli) 게이트라고 부르며, X, Y, Z Gate가 있습니다. T, S, R Gate도 있습니다. 아다마르(Hadamard, H) 게이트가 있습니다. 두 양자 게이트는 CNOT Gate, 3 양자 게이트로는 Toffoli Gate가 있습니다.

양자의 상태는 파동과 위상이 중첩 되어 있다고 했습니다. 그 중 위상을 뒤집어 바꾸는 양자 게이트가 파울리 게이트 입니다. 복잡한 내용으로 들어가기 때문에 대표적인 X Gate만 설명합니다.
SW는 선형대수학으로 Program 하고, HW는 양자연산 장치를 만들어 사용합니다.

양자프로그램에서 행렬곱 선형대수학적으로 X Gate는 X=(10 01)로 표기합니다. 이 X Gate에 | 0 > 을 입력시켜 양자연산을 하면;
Ket 0=(1 0) 이고, Ket 1=(0 1) 이며, X Gate=(10 01) 이므로,
(1 0) * (10 01)=(0 1)=Ket 1이 됩니다.

X Gate는 큐비트의 상태를 뒤집는 작동을 합니다. Ket 0을 Ket 1로 뒤집습니다. 그 반대도 가능합니다.

아주 복잡하고 헷갈리기 쉽습니다. 그러나 주의를 바짝 기울이면 이해가 가게 됩니다.

이것은 SW 선형대수라는 행렬곱으로 나타낸 것이고, 다음 단계 HW 작동 설명이 필요합니다. 위의 선형대수 행렬곱은 머리가 지끈지끈하게 복잡합니다. 상세 설명은 생략합니다.

H Gate는 양자 중첩을 만듭니다. 양자 중첩은 앞에서 설명했습니다.

CNOT Gate는 양자 얽힘을 만듭니다.
양자 얽힘이란 Ket 0 이나 Ket 1 두 개의 같은 상태 큐비트로 서로 얽혀있는 상태를 말합니다. Ket 0이 얽혀있거나, Ket 1이 얽혀있습니다. 따라서 H(아다마르) 게이트를 통하여 얽힌 두 큐비트는, 한 쪽만 측정을 하면 나머지는 측정하지 않아도 동일한 큐비트란 것을 알 수가 있습니다.

그 선형대수 계산은 매우 복잡하여 생략합니다.

양자의 얽힘 상태는 서로 상이한 Ket 0과 Ket 1을 서로 얽히게 할 수도 있습니다. 뒤에 나오는 스핀(Spin, N극과 S극을 가리키는 물성)도 얽히게 할 수 있습니다. 큐비트의 Plus 위상과 Minus 위상도 얽히게 할 수 있습니다.

이런 얽힘의 H Gate는 복잡한 양자연산 회로(Circuit)에 사용됩니다. 바로 양자 통신에 사용됩니다. 한 쪽에서 보낸 큐비트는 상대방에서 그대로 읽을 수가 있는 법입니다.

한쪽에서 보낸 큐비트 상태는 아무리 멀리 떨어져 있어도, 상대방에서 그대로 동시에 읽을 수 있다는 개념만 이해하고 넘어갑니다.

양자 게이트 HW는 무엇으로 만들까요?

고전컴퓨터의 논리와 산술 연산은 ALU가 합니다. 비트 명령어에 따라서 AND, OR, NOT 연산으로 모든 TASK의 연산을 다 해냅니다.

이 HW의 소재는 불순물 혼합 반도체 N형과 P형, 그리고 전류 연결용 구리 전선을 사용합니다. 반도체가 HW의 소재로서 ITC 산업의 주력인 이유가 바로 이것 입니다.

양자연산 X Gate의 HW는 나이오붐(Niobium, Nb, 원자번호 41)이라는 초전도체 전이금속 물질을 사용합니다. 양자 연산체제를 만드는 방법 중 하나인 초전도체에서 사용되지요. 양자 연산에서 양자정보의 흐름은 고전컴퓨터의 전류흐름과는 다릅니다. 바로 양자의 파동을 이용합니다. 따라서 파동이 잘 흐르게 하는 물질들을 사용합니다.

앞의 사전포석 강의에서 굳이 고전컴퓨터의 개념을 설명한 이유도, 이런 양자컴퓨터의 양자연산과 그 소재를 쉽게 이해하도록 하기 위함 입니다.

양자컴퓨터 HW 구성방법인 이온트랩, 광자 편광체, 스핀 시스템 등은 다른 물질을 사용합니다.
이 정도로 양자 게이트 설명을 마칩니다. 나머지 양자 게이트 Y, Z, CNOT, Toffoli 등도 이런 소재와 개념으로 만듭니다.

2-2. 큐비트 만들기
큐비트 Ket 0과 Ket 1은 어떻게 Bit 0과 Bit 1처럼 이진숫자 0과 1을 나타낼까요?

고전컴퓨터의 경우는 트랜지스터(Transistor, TR)의 작동으로 비트 0과 비트 1을 구현했습니다.

양자컴퓨터에서 큐비트 0과 동 1의 구현 방법은 양자컴퓨터 시스템 만드는 방법에 따라 다릅니다. 양자컴퓨터 시스템(System)은 초전도체, Ion Trap, 광자 편광체, 스핀 시스템 등 다양합니다. 이런 시스템을 양자컴퓨터 플랫폼(Flatform) 이라고도 부릅니다.

이중에서 초전도체에서 이용하는 양자 스핀의 개념을 설명합니다.

큐비트 구현을 위해서는 블로흐 구(Bloch Sphere) 라는 새로운 개념을 알아야 합니다.

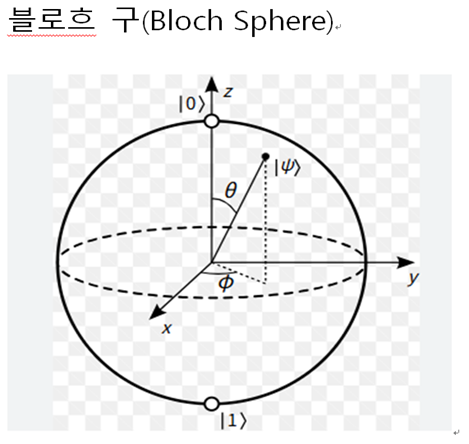
1. 이 구는 반지름 1인 3차원 구를 나타냅니다. XY 평면이 2차원이고 그에 직각인 Z축을 합치면 X Y Z가 3차원을 나타내지요. 양자의 하나인 전자의 궤적은 구름처럼 양성자를 회전합니다. 그 상태는 정원이 아니고 그냥 구름과 같이 회전 하는 것입니다 이 블로흐 구는 전자의 회전 궤적이 정원(正圓)인 것처럼 나타내고 있습니다. 전자 구름회전원을 잘 추리면 정원도 가능합니다.

2. Z축은 양자 스핀이 위쪽=Ket 0과 아래쪽 Ket 1을 나타냅니다

3. X Y축은 Z축에 직각이면서 구의 정중앙(90도)을 자른 궤적으로서 전자의 위상을 나타냅니다. 좌측은 Plus 위상이고 우측은 Minus 위상입니다. 위상은 90도 이외에도 여러 개 나타낼 수가 있지만 확률이 100%에 가까운 것만 필요하기 때문에 Z축이 90도 회전한 XY 2차원 원만 나타낸 것입니다.

4. 프사이(희랍어, 발음 Psi)로 표시한 선분은 양자의 상태(프사이 함수)를 나타냅니다. Z축과 프사이 선분의 각(쎄타)은 정상(正上) Ket 0으로부터 회전한 각도를 의미합니다. 90회전 하면 프사이 상태 확률이 50%로 중첩상태가 됩니다.

5. Y축은 프사이의 위상 정보를 나타냅니다. Y축은 굳이 따지지 않아도, Z축의 Ket 0과 Ket 1 및 X축의 상태 확률 만 이해하면 충분합니다.

큐비트는 블로흐 구로 나타냅니다. Z축 위는 Ket 0 입니다. Z축 아래는 Ket 1 입니다. X Y 축의 위에는 큐비트의 위상 확률을 나타냅니다. 50%에서 100% 구간을 나타내며, 측정을 하면 Ket 0이 됩니다. X Y 축 아래는 역시 50%에서 100% 구간을 나타내며, 측정을 하면 Ket 1이 됩니다. 아마 이해하기 어려울 겁니다. 자세히 읽어보면 알게 됩니다.

이런 양자상태와 그 변동을 SW로는 선행대수 행렬곱으로 계산을 하고, HW는 블로흐 구 형태와 같은 장치를 만들어 큐비트를 표현합니다. 큐비트의 SW 및 HW 개념만 이해하고 넘어갑니다.

2-3. 양자 스핀 이해하기
우리는 앞에서 블로흐 구를 살펴봤습니다. 그 구는 양자인 전자의 구름회전 움직임을 나타내는 개념도 입니다. 개념이지만 양자는 그 블로흐 구에서 설명하는 것과 같은 움직임이나 위상을 가집니다. 그리고 양자 스핀이라는 물성도 가집니다.

양자 스핀(Spin)은 또 뭔가요?

블로후 구의 Z축은 자기장 북(N)과 남(S)을 나타냅니다. 지구의 남과 북은 철의 분자를 남과 북으로 잘 정돈하면, 자석이 이를 가리키게 됩니다.

양자의 스핀(Spin)도 이런 원리를 따릅니다. 양자의 스핀은 불로흐 구의 북쪽과 남쪽을 가리킵니다. Spin-Up과 Spin-Down 이 있습니다. Ket 0은 Spin-Up 이고, Ket 1은 Spin-Down 입니다.
양자 중첩 상태에 마이크로파를 쏘아서, Spin-Up과 Spin-Down을 만듭니다.

Up Spin=Ket 0, Down Spin=Ket 1, 그리고 Up Spin 50% + Down Spin 50%= 양자 중첩이 됩니다.

이런 스핀 조작 방법으로 큐비트를 만드는 것입니다. 큐비트 조작은 양자컴퓨터를 만드는 System에 따라서 다양한 방법이 사용됩니다. 태양빛의 광자(Photon)의 상태로 큐비트를 만드는 시스템도 있습니다. 이 모두를 설명하지 않아도 미루어 이해하면 됩니다.

2-4. 양자컴퓨터 작동 명령어
양자컴퓨터도 고전컴퓨터처럼 양자 게이트 명령어를 사용합니다. 양자게이트 명령어는 X, Y, Z, H, S, T, R, CNOT, SWAP 처럼 양자게이트 명칭으로 명령어를 구성합니다. Z를 치면 큐비트 위상 반전을 합니다. H는 양자큐비트 중첩, CNOT는 양자큐비트 얽힘을 하는 명령어 입니다. SWAP는 두 큐비트 교환을 합니다.

2-5. 양자 레지스터
고전컴퓨터의 연산은 CU가 Memory에서 명령어를 불러와서(Fetch), 이를 해독하여(Read), 레지스터(Register)에 저장해놓고 논리와 산술 연산을 합니다. 그 결과도 이 레지스터에 저장해 놓고 필요하면 꺼내서 사용하기도 합니다.

양자 레지스터는 여러 개의 큐비트를 묶어서 저장하고, 불러와서 연산하는 양자 상태 저장공간 입니다. 큐비트의 중첩도 저장합니다. 이처럼 양자 레지스터는 고전컴퓨터 레지스터와 같은 일을 합니다. 큐비트 2개를 중첩시키면 그 상태는 2의 제곱 4가지 큐비트가 됩니다. |00> |01> |10> |11> 로 나타낼 수가 있습니다.

그러나 4가지 양자상태를 유지하기는 하지만, 그 작동 움직임은 볼 수가 없다는 점이 다릅니다. 눈으로는 볼 수가 없고 양자측정기로 관측하면 양자 상태가 붕괴하지요. 무슨 말이든지 하면 울기만 하는 어린애와 같은 존재입니다.

2-6. 양자 게이트에서 양자 연산하기
양자 회로(Circuit)는 양자컴퓨의 연산 작동을 하는 시스템 입니다.
양자 큐비트 입력을 받아서 양자 게이트의 목적대로 양자 연산을 합니다.

1. X Gate는 큐비트 값을 반전 시킵니다. Ket 0 →Ket 1으로 반전시킵니다. 블로흐 구에서 X축을 180도 회전시키면 Ket 0이 Ket 1이 됩니다.

2. Y Gate는 Y 축을 중심으로 회전하여 양자의 위상이 허수(i)가 되게 합니다. 이 허수의 개념은 양자 얽힘이나 양자 파동의 간섭에 사용되는 선형대수의 한 종류입니다.

3. 아다마르(Hadamard) 게이트는 양자 중첩을 만드는 게이트 입니다.

4. CNOT Gate는 양자 얽힘을 만드는 양자 게이트 입니다.
나머지 게이트의 연산은 그 게이트의 목적에 따라서 작동합니다. 자세한 것은 미루어 알 수 있습니다.

2-7. 양자 연산 회로
양자 연산 회로(Circuit)는 양자컴퓨터 기능을 하나로 연결하여 구성한 양자컴퓨터 시스템 입니다. 그림으로 설명합니다.

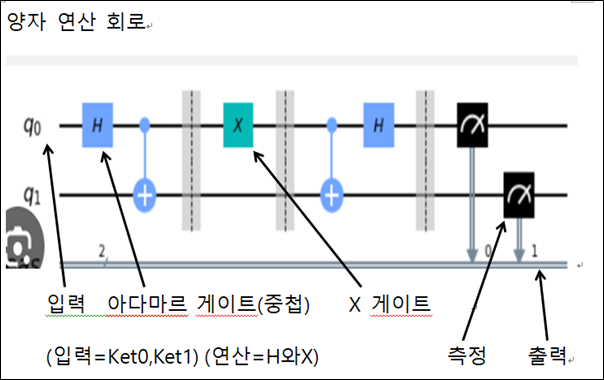
양자 연산은 큐비트를 입력하고 양자 게이를 연결하여 연산을 합니다. 연산이 끝나면 양자 연산결과 측정을 합니다. 측정 결과 큐비트가 나오면 고전 비트로 변환하여 출력 합니다. 그 측정결과는 Ket 0, Ket 1, Ket 0과 Ket 1의 중첩 3가지 입니다.

3. 양자 연산 결과 측정
양자 연산의 결과는 양자 상태로 나타납니다. 바로 볼 수는 없지요. 그 결과를 보기 위하여는 양자 측정(Measurement)을 하여야 합니다. 측정을 하면 양자 상태가 무너져서 Ket 0이나 Ket 1로 나타납니다. 그 상태는 각각의 확률로 나타나지요. Ket 0이 100% 확률이면 Ket 0을 보여줍니다. Ket 1이 100% 확률이면 Ket 1을 보여 줍니다.

양자 측정은 단 한번의 측정으로 이해하면 안 됩니다. 적어도 10번 이상의 측정을 하여야 합니다.

왜 그렇게 하나요?

고전컴퓨터는 단 한번의 연산으로 비트 1인지 비트 0인지를 알 수가 있는데, 그러면 양자컴퓨터가 더 많은 연산을 하니 더 느린 연산이 아닌가요? 양자 컴퓨터의 속도는 양자 측정이 아니고 양자 연산의 속도가 고전 컴퓨터보다 빠르다는 것입니다.

우선 양자연산의 결과 측정은 중첩된 양자 상태 Ket 0과 Ket 1의 확률이 100%가 아니고 Ket 0 70% and Ket 1 30%, 다음에는 Ket 0 60% Ket 1 40% 등 100%에는 가깝지만 각각 다른 결과가 나옵니다. 10번 정도 실시하면 어떤 확률의 경향이 나오지요. 그 결과 100%에 수렴하는 확률로 Ket 0을 정하여, 비트 0으로 결과값을 출력합니다.

비유를 하여 이해하려면 양궁을 보면 쉽습니다. 양자연산 측정은 양궁쏘기 입니다. 10발을 쏘면 10점, 9점, 8점, 7점과 표적외 점수가 나옵니다. 총점 즉 10점이 많으면 이기지요. 양자연산 측정도 양궁점수와 같은 원리로 Ket 0이나 Ket 1의 판정을 합니다.

이런 원리가 바로 양자 출력 과정입니다. 딱 한번으로 100%를 조작할 수는 없지만 여러 번 시행으로 큐비트 0이나 큐비트 1이 되게 조작하는 것이 양자 연산결과 측정 원리입니다.

양자 연산 결과가 측정되면 이를 출력하여 양자 현상을 내용으로 하는 일을 해야 합니다.
예를 들면 신약의 개발에 사용하지요. 신약의 효능확인 Simulation은 양자컴퓨터를 사용하지만, 그 결과로 신약을 만드는 과정에서는 고전컴퓨터를 사용합니다. 이를 위해서 출력 과정에서 큐비트를 고전컴퓨터 언어 비트로 변환하여 사용합니다. 물론 미래에 이 과정도 양자컴퓨터를 사용하도록 기술 개발이 이루어 질 것입니다.

4. 양자 메모리

고전컴퓨터는 그 연산과정과 결과에서 나오는 비트정보를 사용하는 HW로서 Cache, Register, RAM, ROM과 외장 Memory USB, SSD, HDD등 Memory를 사용합니다.

양자컴퓨터는 양자 레지스터를 양자연산 과정에서 사용합니다. 연산 결과나 양자연산 명령어를 저장하는 Memory는 아직 개발 중입니다. 양자 큐비트 저장은 고전 컴퓨터 메모리를 빌려서 사용합니다.

양자 레지스터는 앞의 양자연산 항에서 설명했습니다.

5. 양자 연산 결과 출력

양자 연사 결과 출력은 양자 측정 과정에서 나온 큐비트를 Bit 0이나 Bit 1로 출력 합니다. 양자 연산의 결과를 사용하여 신약개발이나 신소재개발은 고전컴퓨터를 사용하기 때문입니다.

이상으로 양자컴퓨터 알짜배기 큐비트와 양자게이트 및 양자회로를 마칩니다. 양자컴퓨터의 핵심을 다룬 것입니다.

양자 알고리즘으로 이어집니다.

밴드

URL복사