2. 양자컴퓨터의 필요성
고전컴퓨터는 스마트폰이 나오면서 손바닥에 들어갈 정도로 휴대하기 편리하면서 조작하기 쉽고 다양한 연산을 해냅니다.
고전컴퓨터의 디지털화는 비트 1과 비트 0으로 세상의 모든 것을 표현할 수가 있습니다.
이진숫자 1과 0은 비트로 나타냅니다.
문자는 이진숫자로 나타내는 아스키 코드와 유니코드 목록표에서, 해당 문자를 찾아서 이진숫자로 변환하여 나타냅니다.
A는 이진숫자 01000001로 변환하여 사용합니다.
색깔은 RGB 코드를 사용하여 이진숫자로 변환하여 사용합니다.
소리는 그 음정의 높낮이를 숫자화 하고, 이를 이진숫자로 변환하여 사용합니다.
예를 들면 <도레미파솔라시도>를 <12345678>로 숫자화 하고,
이를 이진숫자로 변환하여 디지털화 합니다.
이렇게 변환된 이진숫자로 세상의 거의 모든 물질과 물자를 이진숫자로 나타낼 수가
즉, 디지털화(Digitalization) 할 수가 있는 것입니다.
어떤 업무행동도 업무흐름도(Flowchart)의 과정을 이진숫자로 나타낼 수가 있습니다.
이렇게 디지털화 하는 현상을 디지털 문화라고 부릅니다.
이렇게 세상의 거의 모든 물자나 업무흐름을 이진숫자화 하여 고전컴퓨터로 계산하고 표현할 수가 있는 것입니다.
그렇다면 왜 어려운 양자컴퓨터를 개발하나요?
고전컴퓨터의 핵심 장치인 IC(직접회로)는 반도체 소재를 나노 단위(1십억분의 1단위)로 가공합니다. 현재 3나노 미터 규격은 실제로 사용되고 있으며, 1나노 미터 규격을 개발 중입니다.
물질의 원자 크기는 0.5나노 미터입니다.
고전 컴퓨터는 전자의 움직임이 자아내는 전기의 흐름으로 이진숫자를 생성하여 작동합니다.
물질을 작게 만들어 들어가서 원자 단위가 되면, 그 속의 전자가 깨어져 흘러나옵니다.
깨어져 흘러나오면 컴퓨터 작동이 어렵다는 말입니다.
따라서 원자 단위 물질에 관한 연산에는 고전컴퓨터를 사용할 수가 없습니다.
전자가 깨어지지 않는 새로운 컴퓨터의 개발 필요성이 대두합니다.
신약과 첨단 신소재를 개발하기 위해서는 많은 물질을 융합해야 합니다.
물질의 융합으로 목표로 하는 물성을 찾아내기 위해서는, 그 융합 물질이 새로이 생성해내는 결과 효과를 Simulation으로 확인해야 합니다.
이런 시물레이션은 선형대수와 행렬수학으로 시행합니다. 고전컴퓨터의 연산 능력으로는 신약이나 신소재 개발을 위한 이런 수학을 감당할 수가 없습니다.
그렇지만 양자컴퓨터의 양자연산 능력은 이런 Simulation을 해낼 수가 있습니다.
핵무기 개발, 기상 예측, 주식시세 예측, 암호 해독, 양자정보 통신, 판매사원 단거리 목표점 방문(Travelling Salesman Problem) 문제 등에는 양자 연산이 반드시 필요합니다.
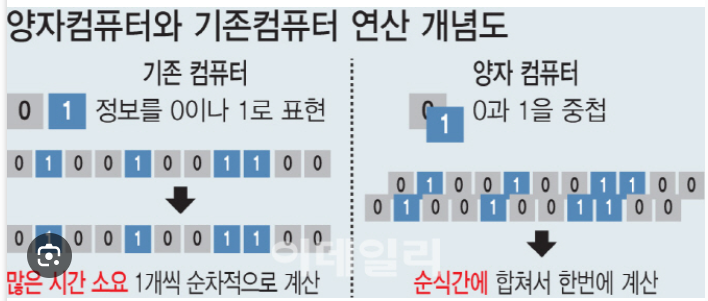
양자 연산은 양자컴퓨터의 양자중첩과 양자얽힘을 활용한 병렬연산(한꺼번에 모든 연산을 실행함)으로 연산시간을 확 줄여냅니다.
양자연산에 사용하는 숫자는 큐비트(Qubit) 입니다.
큐비트는 1개로도 사용하지만 2개, 4개, 10개, 100개, 1천개 등 여러 개를 중첩하여 병렬연산을 할 수가 있습니다.
이렇기 때문에 양자연산이 대단위 선형대수나 행렬수학을 가능하게 하는 것입니다.
큐비트(Qubit)는 | 부호와 Bracket 부호 <, > 를 사용하여 나타냅니다.
( | >)를 Ket 이라고 부르고, (< |) 를 Bra 이라고 부릅니다.
이런 명명법을 디랙 표기법(Dirac Notation) 이라고 합니다.
큐비트는 디랙(브라켓) 표기 외에 행렬(Matrix)로도 표기합니다.
열행렬(세로로 표기)은 Ket에 사용하고, 행행렬은 Bra에 사용합니다.
행행렬은 Bra 0=[1 0], Bra 1=[0 1]처럼 사용합니다,
열행렬은 Ket 0= 1 Ket 1= 0 처럼 표기합니다.
0 1
(1과 0의 세로 수직선은 표시가 안됩니다) 이렇게 양자 컴퓨터는 <큐비트(Qubit) Ket 1>과
<큐비트 Ket 0>의 부호를 만들어 양자 연산에 사용합니다.
출력 단계는 고전 컴퓨터 출력과 같은 전기에너지를 사용합니다. 출력결과 1과 0의 이진 부호가 나타나는 것입니다.
이처럼 양자 컴퓨터는 매우 복잡한 원리, 에너지와 장치를 사용합니다.
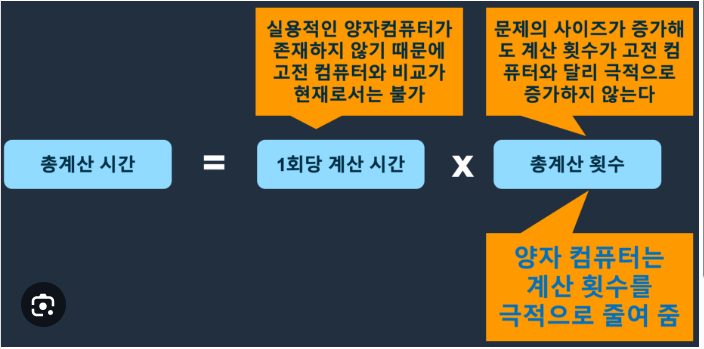
숫자의 사칙연산에는 굳이 양자컴퓨터를 사용하지 않아도 고전컴퓨터로 충분합니다.
그러나 고전적 슈퍼컴퓨터라 하더라도 연산을 해낼 수 없는, 신약개발이나 신소재개발 등을 위해서는 반드시 양자연산을 해야 하는 것입니다.
그런데 이렇게 어려운데 양자역학과 양자정보 비전문가 인 필자의 실력으로 어떻게 이 글을 쓰나요?
새로운 학설을 쓰기는 어려워도 그 책을 읽고 이해하기는 쉬운 편입니다. 학생들은 책을 쓰지는 못하지만, 교과서를 공부하여 이해하고 그렇게 함으로써 익혀 나가는 것입니다.
學而時習之不亦說乎
배우고 때때로 익히면 이 역시 즐겁지 아니 한가? 그 결과 탁월한 글을 쉽게 써낼 수가 있는 것입니다.
양자역학의 공부를 위하여 서점에 있는 거의 모든 책을 공부하면 이해의 문이 열립니다.
김상욱의 양자역학, 퀀텀의 세계, 기초 양자역학, 양자계산과 양자역학, 양자역학-전체와 접힌 질서, 혼자서 풀어보는 양자컴퓨팅, 양자계산과 양자정보, 양자컴퓨팅-이론에서 응용까지, 양자컴퓨터 원리와 수학적 기초, 양자컴퓨팅과 양자알고리즘 개론, 모두를 위한 양자컴퓨터, 암호-비밀을 푸는 과학 등의 책 속에 길이 있는 법입니다.
띄엄띄엄 한 꼭지씩 올리는 본강의를 따라오시면, 시중 서점에서는 구할 수 없는 쉬운 양자컴퓨터 지식이 보일 것입니다.
선형대수나 행렬수학을 배우지 않은 세대라도 이해 가능하게 설명해 나갑니다.
다음 강의는 양자역학 입니다.
